Математика игры в покер Техасский Холдем

Рано или поздно этот день должен был наступить, и вот это случилось. Сегодня мы рассмотрим очень важную тему, которая на первый взгляд может показаться довольно пугающей, особенно для новичков – это математика покера. Однако лишний раз переживать не стоит – математика игры в покер достаточно проста, и далее мы покажем вам несколько элементарных методов расчетов, после прочтения которых вам не нужно будет носить с собой калькулятор, выполняя сложные вычисления и так далее. Поехали!

Интуиция против скилла

Практически все элементы карточной игры построены вокруг математических данных, поэтому навыки правильно их использовать – неотъемлемое качество любого сильного игрока. Существует немало покер-про, которые игнорируют математику, и отталкиваются только от личных аналитических заключений и психологии. Такие люди обладают действительно хорошей интуицией, поэтому покерная математика им попросту не нужна. Тем не менее, помимо собственного опыта и различных вероятностей в покере, иногда и они используют ее при принятии решений для выигрыша. Как правило, такие вычисления позволяют, дескать, немножко «подправить» решения, ранее подсказанные им чутьем.

В истории карточной игры можно привести тысячи случаев, когда профи мирового уровня удивлялись, сколько им могли стоить принятые решение основанные не просто на интуиции, а на математике. Собственно, один из вариантов точно определить, является то или другое решение верным, это проверить посредством математических подсчетов. По-другому друзья никак. Да, возможно в играх со слабым полем эти знания будут лишними, но, если в дальнейшем вы планируете играть в покер на реальные деньги на средних или высоких лимитах, тогда без покерной математики для начинающих никак. Она способна помочь в разных аспектах игры, и сейчас мы рассмотрим ключевые из них. Но сперва небольшой список того, для чего может пригодиться математика – пункты идут в произвольном порядке:

• Вероятности стартовых рук / против рук противника.
• Математическое ожидание.
• Потенциальные шансы рук.
• Подсчет аутов и оддсов.
• Оценка шансов банка.
• Успешный блеф.
• Теория игр.

Вероятности стартовых рук

Начнем с простой математики в покере. При регулярной игре в интернете вы наверняка неоднократно становились свидетелями раздач, которые казались далекими от реальности и не поддавались никаким законам математики. Это друзья теория вероятности, которая работает во многих сферах жизни за пределами карточной игры. Большинство ситуаций несложно определить, если вы будете использовать специальные покер калькуляторы и вспомогательное ПО. Понимая покерные вероятности, вы сможете чаще выигрывать у противников, которые полагаются на госпожу Фортуну. Чтобы не перегружать и без этого нашу непростую статью тоннами различных формул, лучше рассмотрим таблицу с готовыми расчетами, которая точно определяет вероятность попадания разных стартовых рук в комбинацию на префлопе:

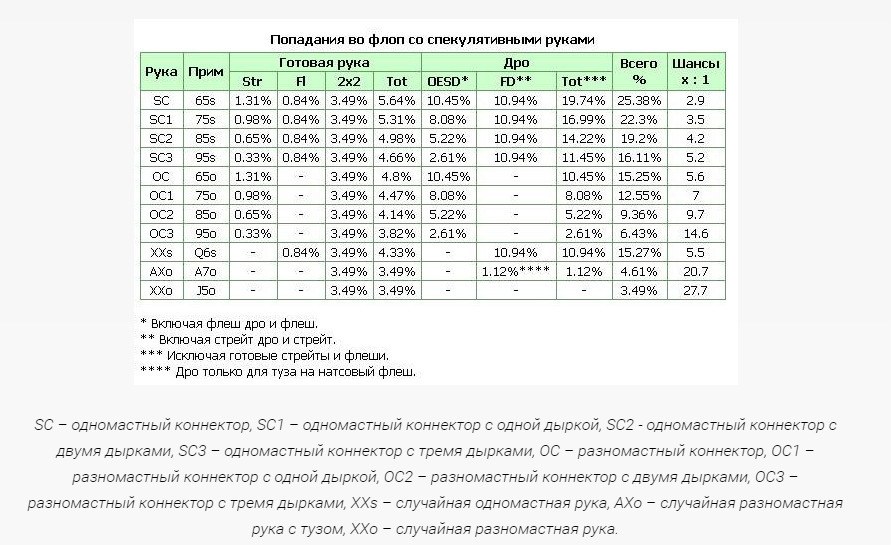
Не переоценивайте стартовые руки, даже если у вас младшие / одномастные карты. Последние не гарантируют то, что вы соберете флеш. Практически то же самое можно сказать про сет – его игрок получает только в 12% случаев. Чтобы обезопасить себя на следующем этапе игры, лучше ознакомиться с различными вероятностями после флопа:

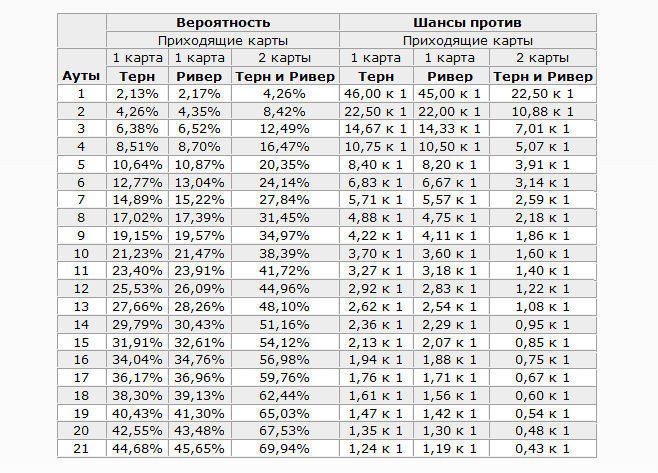
К примеру, если игрок планирует собрать флеш при условии, что в его активе есть четыре одномастные карты, то только 9 общих карт из колоды смогут его выручить. В литературе математики покера от профессионалов называются аутами. Колода содержит по 13 карт каждой масти, исходя из чего можно подсчитать, что 13 – 4 = 9. Если мы получаем флеш-дро на флопе, то у нас 35% вероятность того, что к риверу мы получим пятую по силе комбинацию. Если же после терна вам все равно до флеша не достает одной карты, шанс получить его к риверу равен 20%.

Шансы стартовых рук против рук оппонента

Шансы стартовых рук на флопе, терне и ривере, безусловно, играют очень серьезную роль. При этом если вы нацелены на выигрыши, вам потребуется иметь представление о картах вашего противника (или нескольких). Приведем парочку наглядных примеров, какие шансы имеют стартовые руки против конкретных рук других игроков – обратите внимание, что сегодня мы анализируем исключительно математику Техасского онлайн покера:

• Пара против двух старших карт: 2-2 vs. J-5 (53% и 47%) / 2-2 vs. A-K (53% и 47%).
• Пара против маленькой пары: Q-Q vs. 3-3 (81% и 19%) / Q-Q vs. 10-10 (82% и 18%).
• Пара против старшей и младшей карты: 6-6 vs. K-5 (70% и 30%) / 10-10 vs. A-8 (72% и 28%).
• Две старшие карты против двух младших карт: A-K vs. 7-2 (69% и 31%) / A-K vs. 5-4 (62% и 38%).
• Старшая карта против двух карт среднего достоинства: A-5 vs. K-8 (60% и 40%) / A-5 vs. 10-9 (55% и 45%).

Это далеко не весь перечень возможных расчетов. Отметим, что все они дают только приблизительное понятие о том, что необходимо делать с вашими карманными картами в противостоянии с другими соперниками в Холдеме.

Подсчет аутов

Еще математика покера подразумевает два варианта расчета:

1. Через шансы
2. Через вероятности.

Для первого случая существует два базовых понятия: шанс банка и шанс выпадения аутов. Расчет шанса банка происходит через деление размера банка на сумму ставки. После этого, пользуясь представленной ниже таблицей, игрок может узнать шансы выпадения аута на улицах от флопа до терна, от терна до ривера, и от ривера до флопа. Математика признает EV покериста положительным, если шансы банка будут выше показателей вероятности выпадения аутов:

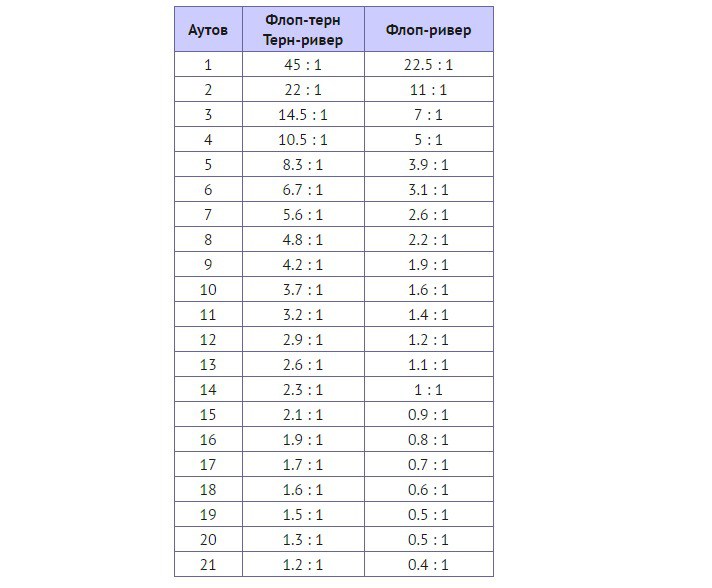
Дисконтированные ауты

Проще говоря, это ауты, которые не просто могут не усилить вашу руку, но могут сделать руку вашего противника еще сильнее. Опираясь на основы математики покера для чайников, мы не можем охватить процедуру дисконтирования аутов в полной мере. Это весьма сложный процесс, на котором «прогорают» даже самые заядлые профи. Сама суть этой процедуры в том, что от совокупного количества аутов игрок должен смотреть ауты, дающие сильную руку, соответственно увеличивающие вероятность выигрыша для оппонента. Ауты желательно дисконтировать регулярно при каждой новой улице, при этом учитывая действия покеристов при выпадении всевозможных карт.

Подсчет оддсов

Оддс представляет собой вероятность появления аута на ближайшей улице. Для этого можно использовать таблицу, которую мы привели ранее, но для похожих ситуаций математика предусматривает расчеты на основе аутов, которые были дисконтированы. На таком этапе многие делают грубые ошибки, поэтому для их избегания нужно внимательно подсчитывать число дисконтированных аутов на предшествующем этапе. Это соотношение шансов банка на ауты покериста на новой улице после дисконтирования.

Математическое ожидание

Как вы уже могли догадаться, немаловажным фактором в игре выступает корректная оценка ситуации и анализ шансов на успех. Грамотные покеристы всегда просчитывают шансы на победу, и приходят к решению о продолжении игры. Важнейшим компонентом покерной математики выступает математическое ожидание (англ. «expected value» / EV). Данный показатель может быть, как положительным, обещая вам выгоду в перспективе (EV+), так и отрицательным (EV-), что значит проигрыш.

Фишка в том, что даже с положительным математическим ожиданием вы можете проиграть в раздаче, но в результате продолжительной катки – отыграетесь и даже выйдете в плюс. Так если вы будете разыгрывать с EV-, тогда вы победите в раздаче, но здесь присутствует доля везения, которая уже в следующий раз может и не принести вам требуемого результата. Чтобы подсчитать EV, требуется умножить предполагаемую выгоду (размер выигрыша) на вероятность выиграть. Далее вам нужно суммировать все умножения. Впрочем, вот как выглядит сама формула: EV = V*Pwin – L*Plose, в которой:

• V – возможный выигрыш.
• P*win – вероятность победы.
• L – возможный проигрыш.
• P*lose – вероятность проигрыша.

Как это правильно сделать? В правилах покерной математики помогает обыкновенный пример со ставкой на бросок монеты. Шансы выпадения орла и решки равны, при этом игрок получит $1 при выпадении орла, и теряет ставку при появлении решки. Подставив значения в формулу, вы получите EV равное нулю: EV = 1*1/2 – 1*1/2 = 0. Очевидно, что нулевое математическое ожидание теряет смысл, но ситуация будет выглядеть иначе, если пари заключается на более выгодных условиях. При появлении орла выплата будет $1,2, а при потере все останется неизменным, так как в подобных условиях EV становится положительным и равно $0,1 (EV = 1,2*1,2 – 1*1/2 = 0,1). Как видите, незамысловатые математические вычисления показывают, почему покеристы желают производить ставки с положительным EV, при этом избегая отрицательных значений. Помните, что, планируя две ставки, выбирайте тот вариант, у которого показатель математического ожидания будет выше.

Шансы банка

Данное значение представляет собой соотношение размера банка, который необходимо получить, к размеру ставки. Узнать это можно с помощью вычисления. К примеру, при ставке в $20, и при желании получить банк в $200, показатель составит 10 к 1. Для ситуаций, при которых шансы банка несколько выше отношения вероятности проигрыша к возможному выигрышу, ставки получат положительное EV. В случаях, когда шансы банка ниже, математическое ожидание будет отрицательным. В описанном случае при шансах банка 10 к 1 ставка будет оправданной при вероятности выигрыша, превышающей 1/11.

Помните, что шансы банка не всегда четко отражают реальную картину, ведь возможный выигрыш может превышать текущие размеры банка. Уже на ближайших раундах торговли ставки покеристов могут значительно умножить банк. В подобных случаях оцениваются потенциальные шансы банка. При этих расчетах важно брать во внимание не текущие размеры банка, а суммировать их с предполагаемыми ставками соперников. К примеру, представим ситуацию на терне с комбинацией 4-7-A-8:

1. Покерист располагает картами K-10, и получает натс флеш-дро.
2. Пока в банке $100, а единственный противник делает ставку в $40.
3. Следует ли производить колл? В подобной ситуации шансы банка равны 3,5 к 1.
4. Покерист знает шесть карт (4 общие и 2 карманные) – получается в колоде еще 46 закрытых карт.
5. Упростить расчет поможет отказ от учета вероятности получения фулл-хауса на ривере.

При таких шансах банка колл будет не оправдан, хотя в то же время, собрав на ривере натс флеш, можно ожидать получение от оппонента дополнительной суммы. Или вот еще одна ситуация – допустим, что в банке $1 000 000. Наша рука имеет шансы 1 к 5. Оппонент ставит $1. Нам лучше сделать колл или сбросить карты? Да, интуиция подсказывает сделать колл по той простой причине, что в большинстве случаев мы останемся ни с чем. Мы рискуем всего $1, и в 20% ситуаций выиграем миллион зеленых.

Как правильно рассчитать шансы банка? Не удивительно, что при продолжительной сессии трудно оценивать все доступные возможности. Шансы на выигрыш оцениваются и по вероятности получения требуемой руки. Сперва покерист подсчитывает общее количество аутов. Делая оценку шансов банка на момент терна, когда нам осталось увидеть одну карту, нужно умножить число аутов на 2. Эти вычисления позволят узнать показатель, который отражает вероятность улучшения руки в %. Так, при 8-ми аутах шансы на улучшение равны 16%, а при 10 – 20%. Для флопа, когда мы ждем еще две карты на доске, расчеты проводятся по аналогии. Исключениями являются только олл-ины – тогда число аутов умножается на 3 и добавляется восемь. Представим, что при 15 аутах мы получим следующие расчеты: 15*3 + 8 = 53. Получается, что вероятность улучшения руки составляет 53%. Также помните, что при количестве аутов менее 8-ми, мы множим на 4, то бишь, если у нас 7 аутов, тогда вероятность будет равна лишь 28%. Несмотря на то, что приведенные расчеты приблизительные, игра показывает, что в большинстве случаев этого оказывается достаточно, чтобы принять оптимальное решение.

Выводы

Будем честны и открыты с вами – ситуации в покере бывают и более сложные. Существует много других аспектов игры, которые можно отнести к математике: вероятности в покере, успешный блеф, шансы рук, оценка диапазонов и размеров стеков для поздних улиц, шансы банка, эквити и так далее. Покерная математика может усложняться до бесконечности, и даже самые сильные игроки могут не знать всех тонкостей и аспектов. Несмотря на это, в нашем случае подобные нюансы ни к чему, ведь даже элементарное понятие некоторых основ покерной математики, о которых мы рассказали вам выше, поможет сделать наши дальнейшие решения значительно лучше и эффективнее. Учитесь, практикуйтесь, развивайтесь, и у вас все выйдет. А чтобы ваша игра стала еще более выигрышной, воспользуйтесь бездепозитным бонусом в размере $88 от 888Poker и применяйте полученные знания на деле не просто в игре на условные фишки, а на реальный кэш.